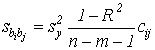 .
.Изощренная методика отбраковки незначимых показателей была разработана для решения вырожденных или почти вырожденных задач (при наличии мультиколинеарности или плохой обусловленности матрицы системы нормальных уравнений). Поставленная цель, в конце концов, была достигнута, и методика пошаговой регрессии с дополнительной проверкой вырождения на каждом шаге считается сейчас неотъемлемой составной частью алгоритма современного регрессионного анализа.
Но как только усилиями многих специалистов проблема вырождения была разрешена, тут же были высказаны сомнения в правильности самого пути преодоления возникших затруднений.
Уверены ли мы в том, что в принципе допустимо выбраковывать часть переменных из модели? Ведь совокупный эффект был предопределен влиянием всех показателей, а мы, произвольно отбрасывая часть членов, все приписываем оставшимся в модели переменным и, тем самым, искажаем их истинный вклад. Приведем конкретный пример, где подобный подход все доводит до абсурда.
Обычно в сельском хозяйстве применяются комбинированные удобрения (NPK) с внесением азотных (N), фосфорных (P) и калийных (K) удобрений в определенной пропорции. Пусть мы располагаем данными об урожайности некоторой культуры от возрастающих доз комбинированного удобрения NPK. Возможно ли по таким данным выделить отдельно эффекты каждой составляющей N, P, K? Ну, конечно же, нельзя. Компоненты N, P, K в этой задаче связаны точной линейной зависимостью и при подключении в модель одной компоненты (любой) процесс подключения автоматически завершится. При этом весь совместный вклад трех видов удобрений будет целиком приписан только одной компоненте, которую метод подключения случайным образом изберет первой. Относительно оставшихся (не подключенных в модель показателей делается стандартное (и совершенно неверное) заключение типа: “... в данных почвенно-климатических условиях (почему-то) не проявилось действие некоторых видов удобрений...”.
Поэтому параллельно с доводкой алгоритма выбраковок разрабатывались также и другие пути преодоления вырождений. Некоторые из них привели к одному и тому же результату, хотя применялась разная аргументация и совсем не похожие математические преобразования. Перечислим несколько таких эквивалентных методик: псевдообратной матрицы, главных компонент, сингулярного разложения. (Сразу же оговоримся, вышеперечисленные методики эквивалентны только в вопросе разрешения проблемы вырождения, а так вообще они предназначены для решения разных задач и никоим образом не подменяют друг друга целиком).
Чисто технически алгоритм МНК с применением псевдообратной матрицы выглядит так. Требуется решить систему нормальных уравнений, которую в матричной форме можно записать следующим образом:
Ab = XTY ,
где
A = XTX .Если матрица
A - невырожденная, то для нее существует обратная матрица C=A-1 и искомое решение, а также дисперсии и ковариации коэффициентов регрессии выражаются через элементы этой обратной матрицы:b
= A-1XTY = CXTY ;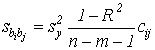 .
.
В случае вырождения предлагается обратную матрицу
A-1 (и ее элементы) во всех приведенных выше формулах заменить на так называемую псевдообратную (“обобщенную обратную”) матрицу A-, для которой всегда имеют место соотношения:AA-A = A
;A-AA- = A- .
Никаких выбраковок при этом делать не надо.
При отсутствии вырождения автоматически получается стандартное решение.Конечно, получить псевдообратную матрицу намного сложнее, чем просто обратить матрицу системы нормальных уравнений (с попутной выбраковкой взаимосвязанных показателей), но для этого существует соответствующее программное обеспечение.
Прежде чем приступить к детальному изучению алгоритма с псевдообратной матрицей, обсудим свойства нового обобщенного решения, которые нам могут и не понравиться.
При вырождении система нормальных уравнений имеет не одно определенное, а бесчисленное множество решений (так как система нормальных уравнений всегда совместна). С помощью псевдообратной матрицы выделяется решение с наименьшими значениями коэффициентов регрессии (в модель включаются все переменные и общий вклад “размазывается” по большому числу членов модели). Но малое значение коэффициента регрессии, как правило, означает малую его значимость по критерию Стьюдента. Не получится ли так, что новое обобщенное решение будет значимо в целом (по критерию Фишера), но состоять только из незначимых членов?Ну, что же, анализ данных очень часто представляет собой небольшое научное исследование и полезно рассмотреть проблему со всех сторон, насколько нам позволяют наши знания и умение.
Ниже нам понадобятся некоторые сведения из теории матриц, понятие ортогональной матрицы и хотя бы поверхностное знакомство с проблемой собственных векторов и собственных чисел симметричных квадратных матриц. Нет смысла слишком углубляться в эти вопросы, достаточно знать, что все вычислительные алгоритмы реализованы на ЭВМ.
Итак, напоминаем.
Произведение матрицы
A на вектор X (вектор - это матрица-столбец) означает преобразование исходного вектора X в новый вектор: Y=AX. Поскольку любой вектор может быть разложен по системе координатных, достаточно рассмотреть преобразование этих координатных векторов: I1 = (1, 0, 0, ..., 0)T ; I2 = (0, 1, 0, ..., 0)T и т.д. до Im = (0, 0, 0, ..., 1)T . Нетрудно непосредственно убедиться, что преобразованные координатные векторы представляют собой столбцы матрицы A: AIk = Ak (напоминаем, что матрицы перемножаются по правилу “строка на столбец").Разным матрицам соответствуют различные линейные преобразования векторного пространства. Среди этих преобразований выделим
"ортогональные" преобразования, которые не изменяют ни длин векторов, ни углов между ними (к ортогональным преобразованиям относятся всевозможные повороты и зеркальные отражения объектов). По виду матрицы A можно сразу установить, является ли преобразование с этой матрицей ортогональным: для этого необходимо, чтобы новая система координатных векторов (столбцы матрицы A) осталась ортонормированной (суммы квадратов элементов любого столбца равны единице, суммы произведений элементов любых двух столбцов равны нулю). Отсюда следует, что для ортогональных матриц имеет место соотношение ATA = I, где I - единичная матрица. Иными словами, транспортирование ортогональной матрицы приводит к ее обращению AT = A-1. Ввиду коммутативности произведения взаимообратных матриц для ортогональных матриц получаем также ATA = AAT = I .Единичная матрица является частным случаем диагональных матриц, в которых отличны от нуля только элементы на главной диагонали:
Dl ={l 1 , l 2 , ... , l m} .
Любую симметричную квадратную матрицу
A можно представить в виде произведения матричных сомножителейA = UDl UT
,где l
i - так называемые "собственные" или “характеристические" числа, а U - ортогональная матрица собственных векторов.Если матрица
A - невырожденная, то все ее собственные числа отличны от нуля. Нетрудно убедиться, что в этом случае матрица![]()
является обратной к матрице
A.Решение системы нормальных уравнений с невырожденной матрицей можно записать в виде:
![]() .
.
Если матрица
A - вырожденная, то одно или несколько ее собственных чисел (последних) равны нулю. Рассмотрим систему нормальных уравнений с такой матрицей:A b = UDl UT b = XTY .
Умножим это матричное равенство слева на
UT, учтем, что UTU = I, и временно переобозначим UTXTY = Z , UT b = d . Получим такую систему уравнений: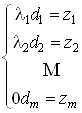 .
.
Здесь (для примера) принято, что последнее собственное число равно нулю (l
m = 0); ввиду совместности системы нормальных уравнений автоматически получится zm = 0.Решаем эту систему:
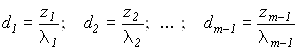
dm -произвольное.
Если положить произвольное значение dm нулю, то вектор d будет иметь минимально возможную длину. Поскольку вектор коэффициентов регрессии b = U d получается ортогональным преобразованием из вектора d, его длина будет той же самой, т.е. минимально возможной.
Чтобы записать решение в матричной форме, введем обозначения:
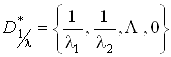 .
.
Здесь по диагонали стоят числа, обратные ненулевым собственным числам матрицы
A; остальные элементы матрицы - нули. Тогда![]() ;
;
![]() .
.
Для сопоставления с невырожденным решением введена матрица
![]() ,
,
которая является псевдообратной (обобщенной обратной) к матрице
A (непосредственно убеждаемся, что AA-A = A и A-AA- = A-). Если все собственные числа отличны от нуля, то A- = A-1.Представим, что все собственные числа отличны от нуля, но одно или несколько чисел близки к нулю. Пусть l
m » 0. Ввиду совместимости системы нормальных уравнений автоматически получится, что zm » 0 и формально можно вычислить компоненту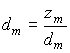 . Здесь и числитель и знаменатель близки к нулю, т.е. это выражение напоминает раскрытие неопределенности типа “нуль на нуль"
. Здесь и числитель и знаменатель близки к нулю, т.е. это выражение напоминает раскрытие неопределенности типа “нуль на нуль" Дополнение: Метод главных компонент
Если исходные переменные-аргументы связаны тесными мультиколинеарными соотношениями, то это означает, что либо эти переменные взаимно определяют друг друга, либо же они являются разными следствиями неких общих причин - агрегированных показателей (факторов). Возникает идея, а нельзя ли
"сжать" информацию, содержащуюся в массиве наблюдений большого числа взаимнокоррелированных переменных, заменив их на меньшее число независимых агрегированных показателей-факторов.Заменим исходную систему переменных
x1 , x2 , ... , xm на некие их линейные комбинации (компоненты):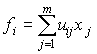
где
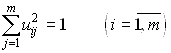 .
.
Пусть все исходные переменные будут стандартизованными, следовательно, их дисперсии одинаковы и равны единице; иными словами, в результате нормировок (стандартизации) все переменные выровнены по своей изменчивости. Компоненты будем составлять по следующему экстремальному принципу. Потребуем, чтобы первая компонента имела максимально возможную дисперсию, т.е. объясняла максимум суммарной изменчивости исходных переменных; вторая компонента, некоррелированная к первой, объясняла максимум оставшейся дисперсии, и т.д. При таком подходе несколько первых (главных) компонент будут объяснять почти всю изменчивость системы, а последние компоненты с дисперсиями, близкими к нулю, можно отбросить, так как они фактически не варьируют.
Оказывается, набор коэффициентов
uij для каждой компоненты образует собственный вектор корреляционной матрицы (матрицы системы нормальных уравнений), а соответствующее ему собственное число l i равно дисперсии i-ой компонентыСоставляем уравнение регрессии относительно главных компонент
:y = d1 f1 + d2 f2 + ... + dk fk + e ,
где
k £ m - число главных компонент. Ввиду некоррелированности компонент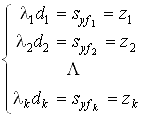 .
.
Получаем вектор
d - вектор коэффициентов регрессии в разложении результативного признака по главным компонентам. Осталось подставить вместо компонент их выражения через исходные переменные и перегруппировать члены, что эквивалентно матричному преобразованию b=U d .Таким образом, временным переходом к системе главных компонент обходят все затруднения, связанные с вырождениями. Другие приложения главных компонент составили содержание нового статистического анализа - так называемого,
"факторного анализа".Дополнение: Метод сингулярного разложения матриц
(SVD)Неустранимые погрешности могут появиться на самом первом этапе стандартного МНК - на этапе составления системы нормальных уравнений.
Рассмотрим пример Дж. Форсайта аппроксимации динамики роста населения США квадратичной моделью:
y = b0 + b1
t + b2t2 + e ,где
t — последовательные годы (т.е. числа порядка 2000) за 20-летний период.Составляем систему нормальных уравнений для квадратичной модели:
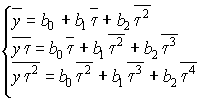 .
.
Здесь коэффициенты нормальной системы имеют порядок от а
11 = 1 до а33 » 20004 = 16× 1012, причем недопустима никакая потеря младших разрядов. Дж. Форсайт показал, что расчет этого примера на ЭВМ даже с двойной точностью не приводит к правильной аппроксимации зависимости квадратичной моделью.Конечно, затруднения именно этого примера легко преодолеваются - достаточно в качестве
t задать последовательные номера (без сотен и тысяч лет); еще лучше предварительно центрировать переменную t ; наконец здесь достаточно просто можно произвести ортогонализацию членов квадратной модели. Однако предупреждение Дж. Форсайта остается в силе - существуют ситуации, когда сам переход к системе нормальных уравнений может привести к потере точности. Мы настолько привыкли составлять и решать систему нормальных уравнений для минимизации суммы квадратов невязок, что сама мысль о том, что этот путь не является единственно возможным (и даже не наилучшим), кажется неожиданной. Несколько десятилетий назад, когда все расчеты выполнялись вручную, другого пути реализации МНК практически не существовало, но сейчас, при доступности персональных компьютеров, при наличии таких пакетов прикладных программ, как Матлаб или Статграф, просто желательно рассматривать решение системы нормальных уравнений всего лишь как первое приближение, которое подлежит дальнейшему уточнению. И нередко специалист с изумлением убеждается, что стандартные МНК-оценки параметров были получены с большими смещениями (см. также пример в лекции 8).В методе
SVD Дж. Форсайта используется возможность представления любой прямоугольной матрицы размером n ´ m в виде произведения (сингулярного разложения):X = VD6UT
,где
U - ортогональная матрица размера m´ m; V - ортогональная матрица размера n´ n; D6 - ортогональная матрица размера n´ m, в которой отличны от нуля не более m элементов по главной диагонали.Нетрудно убедиться, что матрица
U состоит из собственных векторов матрицы XTX, матрица V состоит из собственных векторов матрицы XXT, квадраты чисел s i2 = l i есть собственные числа матрицы XTX (и ненулевые собственные числа матрицы XXT).Согласно МНК, требуется найти решение следующей переопределенной системы уравнений
Y = X b + E
Из условия минимума суммы квадратов вектора Е.
Заменим в этом матричном равенстве матрицу Х на ее сингулярное разложение.
Y = V D6UT b + E ,
умножим равенство слева на
VT и введем обозначения: W=VTY; O=VTE; UT b=d . Получим: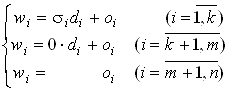 .
.
Здесь
k - количество ненулевых чисел s i (k£ m). Ввиду ортогональности матрицы V суммы квадратов элементов векторов E и O одинаковы, причем можно первые k элементов вектора O сделать равными нулю, полагая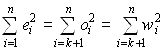 .
.
При наличии мультиколинеарности несколько последних чисел s
i равны нулю (или близки к нулю), поэтому последние компоненты вектора d могут принимать любые значения. Положим их нулю, тем самым получим решение с наименьшими значениями коэффициентов регрессии. Ортогональное преобразование b=U d с матрицей U не изменяет величины суммы квадратов коэффициентов регрессии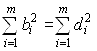 .
.
При наличии соответствующего программного обеспечения (например, ППП Матлаб) рекомендуется во всех случаях вместо стандартной процедуры МНК использовать более надежную процедуру
SVD.Обсудим проблемы мультиколинеарности и вырождения матрицы, а также дополним алгоритм подключения-исключения необходимыми контролями.
Сначала разберем критерий мультиколинеарности Феррара-Глобера и убедимся, что он ничего не дает. Согласно этому критерию, надлежит вычислить для каждой переменной коэффициенты детерминации 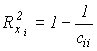 и проверить значимость самой тесной внутренней корреляционной связи между переменными-аргументами по критерию Фишера:
и проверить значимость самой тесной внутренней корреляционной связи между переменными-аргументами по критерию Фишера:
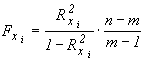 .
.
Здесь
m - число подключенных переменных; cii - диагональные элементы обратной матрицы.Для нашего примера (см. предыдущие лабораторные работы) имеем:
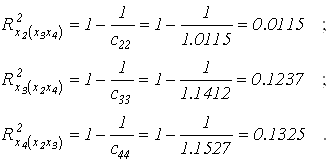
Вычисляем дисперсионное отношение для наибольшего коэффициента детерминации
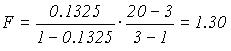 .
.
Это значение оказалось меньше табличного
F0.05(2,17)=3.59, поэтому все внутренние корреляционные связи при n=20 признаются незначимыми. Однако, если бы n было бы не 20, а 200, то та же самая мультиколинеарная связь была бы уже значимой, так как в этом случае дисперсионное отношение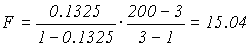
уже значительно превышает верхнюю границу
F0.01(2,197)=4.60 .Ну, и что из этого следует? Хоть что-нибудь изменилось в наших представлениях? Мы и так не сомневались в том, что переменная
x4 коррелирует с переменой x3Известно, что МНК допускает существование значимых мультиколинеарных связей между показателями-аргументами, лишь бы эти связи не были слишком тесными, а определитель нормальной системы не был близок к нулю.
Критерий Феррара-Глобера оценивает значимость внутренних связей между членами модели, а не степень вырожденности корреляционной матрицы, а ведь нас интересует только это. Не ту сторону явления освещает критерий Феррара-Глобера, не разрешает он поставленной проблемы. Настоящий критерий мультиколинеарности должен бы оценивать допустимость (или недопустимость) существующей тесноты внутренней связи, но не с точки зрения ее
статистической значимости или незначимости; статистические представления здесь вообще ни при чем.Теперь рассмотрим второй важный аспект поставленной проблемы. Как уже упоминалось выше, в процессе подключения дополнительных членов иногда наблюдается явление “ прохлопывания” , когда после подключения в модель очередного члена часть коэффициентов (или даже все коэффициенты) регрессии резко меняют свои значения (они могут изменить даже знаки). Эффект этот был замечен не только при обработке статистических данных, но также при аппроксимации функций при достижении некоторого критического числа членов модели. Неизвестно, связан ли эффект “ прохлопывания” с вырождением матрицы, но он является отличительным признаком наличия мультиколинеарности. Что-то подобное нам встретилось (см. предыдущую лабораторную работу) при составлении сопряженой модели, когда в качестве результативного признака была выбрана переменная
x4 . В табл. 9.1 продублирована корреляционная матрица, где переменная y переобозначена через x0 , чтобы она не отвлекала внимание своим внешним видом.Таблица 9.1
Корреляционная матрица
|
x0 |
x1 |
x2 |
x3 |
x4 |
|
|
x0 |
1 |
0,35 |
0,81 |
-0,46 |
0 |
|
x1 |
1 |
0,35 |
-0,10 |
0 |
|
|
x2 |
1 |
0 |
-0,10 |
||
|
x3 |
1 |
0,35 |
|||
|
x4 |
1 |
Как видно из корреляционной матрицы,
Мы располагаем уже выполненными тремя последовательными итерациями:
![]() ;
;
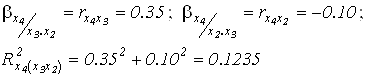
(переменные
x2 и x3 не коррелируют между собой, поэтому их вклады просто суммируются) .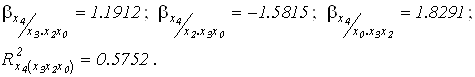
Результаты последнего расчета взяты из расширенной обратной матрицы (табл. 7.1, строки 24-28).
При подключении переменной
x0 предыдущие b -коэффициенты резко изменились; переменная x0 оказалась значимой, ее вклад в несколько раз превышает вклад обоих ранее включенных членов. Интересно, что мультиколинеарные связи совершенно скрыли это влияние x0 , оно проявилось только при фиксировании на постоянном уровне переменных x2 , x3 (сравнитеВыделим этот странный эффект “ прохлопывания” в чистом виде.
Рассмотрим разложение переменной
x3 по x0 и x2 (разложение многомерного вектора x3 по базису x0 , x2); все переменные предполагаются стандартизированными: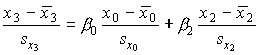 .
.
Составим систему нормальных уравнений
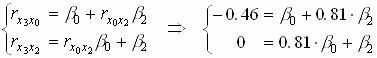
и решим ее: b
0 = -1.3376; b 2 = 1.0834 .Оба b -коэффициента оказались по модулю больше единицы.
Коэффициент детерминации (вклад двух переменных
x0 , x2)![]()
значительно превышает вклад только одного показателя
x0 (Дадим геометрическую интерпретацию полученным результатам. После стандартизации все “многомерные вектора” имеют одинаковую “длину”. Могут ли проекции единичного вектора
x3 при разложении по единичному базису (x0 , x2) быть больше единицы (по модулю)? Конечно, нет, если базис ортогональныйj 02 = arccos 0.81 = 35.9°
;j 03 = arccos (-0.46) = 117.4° ;
j 23 = arccos 0 = 90° .
На рис. 9.1 изображена плоскость, проходящая через единичные вектора
x0 , x2 (угол между которыми j 02 = 35,9° ). Вектор x3 не лежит в этой плоскости, его проекция на координатную плоскость располагается где-то в заштрихованной области (в секторе между 117.4° и 90° + 35.9° = 125.9° ). Его длина равна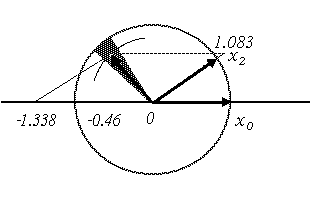
Рис. 9.1. Разложение вектора по косоугольному базису
Итак, при разложении единичного вектора по единичному, но не ортогональному, базису косоугольные проекции могут быть большими единицы (по модулю). Иными словами, из-за внутренних (вполне допустимых) мультикорреляционных связей между членами модели в уравнении регрессии могут появиться b
-коэффициенты большие единицы, причем это происходит на этапе подключения какой-то очередной переменной. С точки зрения математики здесь все в порядке. Модель с такими значениями b -коэффициентами правильно воспроизводит значения результативного признака. Интересно, что эффект “ прохлопывания” оказался не связанным с вырождениями. Пока мы не располагаем никакими критериями, которые бы предупреждали нас о возможности появления рассмотренного эффекта (а может быть, и не нужны такие критерии?).Теперь, разберем проблему вырождения, плохой обусловленности, неустойчивости решения, а также внесем некоторые коррективы в алгоритм подключения-исключения.
При подключении в модель очередного показателя
xi уменьшается не только остаточная дисперсияДиагональные элементы
sii - есть дисперсии невязок при разложении каждой не включенной еще в модель переменной по системе уже учтенных показателей. Представим себе, что одна из оставшихся вне модели переменных xk практически точно описывается учтенными показателями, тогда все ее невязки являются всего лишь малыми ошибками и, следовательно, ее дисперсия и все ее частные ковариации с другими оставшимися вне модели переменными будут также близки к нулю: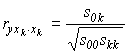 и числитель, и знаменатель будут близки к нулю, но значение коэффициента частной корреляции может быть каким угодно, в том числе и близким к единице. В этом случае наш алгоритм подключит в модель переменную xk с разрешающим элементом skk »
0, близким к нулю, в результате чего элементы обратной матрицы резко возрастут; очень часто при этом проявляется эффект “
прохлопывания”
, при котором b
-коэффициенты изменяются совершенно произвольным образом. Предлагаем дополнить алгоритм подключения следующим элементарным контролем: если какой либо диагональный элемент skk окажется меньше, скажем, 5% исходной величины (т.е. меньше 0.05), то такую переменную xi следует исключить из дальнейшего анализа. Это правило надо распространить и на результативный признак: - если s00 < 0. 05 , то процесс дальнейшего подключения надо прервать, так как новым переменным уже нечего объяснять.
и числитель, и знаменатель будут близки к нулю, но значение коэффициента частной корреляции может быть каким угодно, в том числе и близким к единице. В этом случае наш алгоритм подключит в модель переменную xk с разрешающим элементом skk »
0, близким к нулю, в результате чего элементы обратной матрицы резко возрастут; очень часто при этом проявляется эффект “
прохлопывания”
, при котором b
-коэффициенты изменяются совершенно произвольным образом. Предлагаем дополнить алгоритм подключения следующим элементарным контролем: если какой либо диагональный элемент skk окажется меньше, скажем, 5% исходной величины (т.е. меньше 0.05), то такую переменную xi следует исключить из дальнейшего анализа. Это правило надо распространить и на результативный признак: - если s00 < 0. 05 , то процесс дальнейшего подключения надо прервать, так как новым переменным уже нечего объяснять.
В этом рекомендуемом дополнении алгоритма не ясно только одно - почему надо принять в качестве критического значения
skk именно 5% исходной величины, а не другие границы в каждом конкретном случае. Обоснуем эту рекомендацию.Хотелось бы знать, к каким неприятным последствиям приведет включение в модель той или иной переменной. Будем оценивать степень неустойчивости получаемого решения после каждой итерации процесса подключения: к каким погрешностям в решении могут привести малые ошибки в исходных коэффициентах системы нормальных уравнений.
Поскольку определитель квадратной матрицы
A можно разложить по элементам любой строки D=|aij| = ak1 Ak1 + ak2 Ak2 + ... + akn Akn , то частные производные определителя по любому элементу матрицы будут равны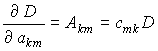
где
Akm - алгебраические дополнения, которые выражаются через элементы обратной матрицы cmk .Таким образом, относительная погрешность определителя при изменении элемента
akm на величину D akm будет равна cmk.D akm .Продемонстрируем это на примере обращения плохо обусловленной матрицы Гильберта, элементы которой составляются по принципу
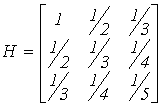
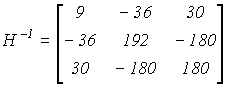 .
.
При обращении в рациональных числах не встретится никаких затруднений.
Теперь округлим все элементы матрицы Гильберта до трех десятичных знаков и обратим ее со всей возможной точностью (можно на ЭВМ). Получим
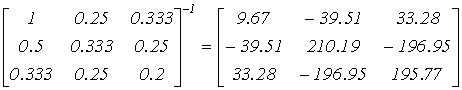 .
.
Совершенно ничтожные ошибки округления в коэффициентах
a13 , a22 , a31 (абсолютная погрешность D a13 = D a22 = D a31 = 1/3000; относительная погрешность менее 0.1%) привели к заметным погрешностям в элементах обратной матрицы (сравни c33 = 195.77 c точным значением 180).Оценим последствия малых изменений элементов матрицы
a13 , a22 , a31 по предлагаемой выше методике. Вычислим ожидаемую относительную погрешность определителя: (c31 + c22 + c13)× D a13 = -(33.28 + 210.19 + 33.28) / 3000 = -0.09 (т.е. 9%).Результирующая погрешность возросла в
270 раз по сравнению с погрешностью в исходных коэффициентах (сравните 9% и 100/3000=1/30% )!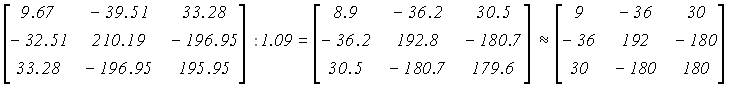 .
.
Мы получили элементы, довольно близкие к точным значениям, и могли бы еще более улучшить решение, так как мы учли погрешность только одного определителя системы, а элементы обратной матрицы есть отношение двух определителей.
Итак, мы имеем возможность оценивать последствия малых погрешностей в исходных коэффициентах (т.е. оценивать степень неустойчивости решения). Применительно к нашей задаче заметим, что все исходные коэффициенты корреляции (коэффициенты нормальной системы) вычислялись с четырьмя
знаками после запятой; один знак считается резервным, поэтому разумно предположить, что погрешности недиагональных элементов исходной матрицы не превосходят по модулю единицы третьего знака, т.е. 0.001. Следовательно, относительную погрешность решения не будет превосходить2× (0.0403 + 0.1153 + 0.4034)× 0.001=1.118× 0.001» 0.0011
оказалась того же порядка, что и исходные погрешности в коэффициентах системы. В процессе подключения все разрешающие элементы были отличны от нуля (в табл. 6.7 разрешающие элементы взяты в рамочку), никакого вырождения здесь не встретилось, поэтому исходные погрешности не увеличились. А вот в одном из вариантов метода подключения-исключения нам пришлось обращать расширенную матрицу, причем на одном из этапов мы произвели преобразование Жордана-Гаусса с разрешающим элементом
s00=0.0648, близким к критической границе 0.05. Элементы обратной матрицы при этом заметно возросли (см. табл. 7.2). Оценим возможные последствия. Относительная погрешность всех дальнейших результатов здесь может достигать величины2× (12.93 + 8.60 + 4.31 + 7.25 + 3.72 + 2.80)× 0.001=79.22× 0.001=0.079 » 8%
.Исходные погрешности увеличились в
80 раз! Погрешность в 8% уже заметная (хотя еще терпимая). При меньших же величинах разрешающего элемента (меньших 0.05) относительная погрешность будет уже порядка (10¸ 15)% , что уже считается недопустимым.Таким образом, мы разобрали все детали алгоритма подключения-исключения, дополнили алгоритм проверками устойчивости решения и предложили удобную вычислительную схему, требующую для реализации алгоритма не больше операций, чем для обычного обращения матрицы.